
伯努利方程(Bernoulli equation)
理想正壓流體在有勢(shì)徹體力作用下作定常運(yùn)動(dòng)時(shí),運(yùn)動(dòng)方程(即歐拉方程)沿流線積分而得到的表達(dá)運(yùn)動(dòng)流體機(jī)械能守恒的方程。因著名的瑞士科學(xué)家D.伯努利于1738年提出而得名。對(duì)于重力場(chǎng)中的不可壓縮均質(zhì)流體 ,方程為
p+ρgz+(1/2)*ρv^2=C
式中p、ρ、v分別為流體的壓強(qiáng)、密度和速度;z 為鉛垂高度;g為重力加速度。
上式各項(xiàng)分別表示單位體積流體的壓力能 p、重力勢(shì)能ρg z和動(dòng)能(1/2)*ρv ^2,在沿流線運(yùn)動(dòng)過(guò)程中,總和保持不變,即總能量守恒。但各流線之間總能量(即上式中的常量值)可能不同。對(duì)于氣體,可忽略重力,方程簡(jiǎn)化為p+(1/2)*ρv ^2=常量(p0),各項(xiàng)分別稱為靜壓 、動(dòng)壓和總壓。顯然 ,流動(dòng)中速度增大,壓強(qiáng)就減小;速度減小, 壓強(qiáng)就增大;速度降為零,壓強(qiáng)就達(dá)到最大(理論上應(yīng)等于總壓)。飛機(jī)機(jī)翼產(chǎn)生舉力,就在于下翼面速度低而壓強(qiáng)大,上翼面速度高而壓強(qiáng)小 ,因而合力向上。 據(jù)此方程,測(cè)量流體的總壓、靜壓即可求得速度,成為皮托管測(cè)速的原理。在無(wú)旋流動(dòng)中,也可利用無(wú)旋條件積分歐拉方程而得到相同的結(jié)果但涵義不同,此時(shí)公式中的常量在全流場(chǎng)不變,表示各流線上流體有相同的總能量,方程適用于全流場(chǎng)任意兩點(diǎn)之間。在粘性流動(dòng)中,粘性摩擦力消耗機(jī)械能而產(chǎn)生熱,機(jī)械能不守恒,推廣使用伯努利方程時(shí),應(yīng)加進(jìn)機(jī)械能損失項(xiàng)。
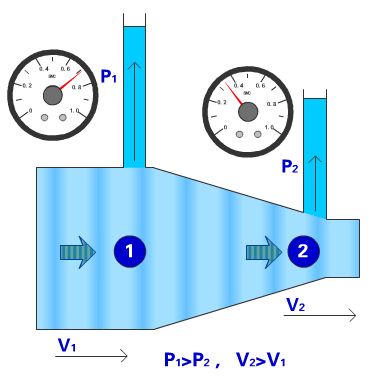
圖為驗(yàn)證伯努利方程的空氣動(dòng)力實(shí)驗(yàn)。
補(bǔ)充:p1+1/2ρv1^2+ρgh1=p2+1/2ρv2^2+ρgh2(1)
p+ρgh+(1/2)*ρv^2=常量 (2)
均為伯努利方程
其中ρv^2/2項(xiàng)與流速有關(guān),稱為動(dòng)壓強(qiáng),而p和ρgh稱為靜壓強(qiáng)。
伯努利方程揭示流體在重力場(chǎng)中流動(dòng)時(shí)的能量守恒。
由伯努利方程可以看出,流速高處壓力低,流速低處壓力高。
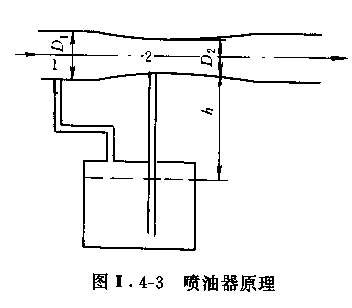
圖II.4-3為一噴油器,已知進(jìn)口和出口直徑D1=8mm,喉部直徑D2=7.4mm,進(jìn)口空氣壓力p1=0.5MPa,進(jìn)口空氣溫度T1=300K,通過(guò)噴油器的空氣流量qa=500L/min(ANR),油杯內(nèi)油的密度ρ=800kg/m3。問(wèn)油杯內(nèi)右面比喉部低多少就不能將油吸入管內(nèi)進(jìn)行噴油?
解:
由氣體狀態(tài)方程,知進(jìn)口空氣密度ρ=p1/(RT1)=(0.5+0.1)/(287*300)kg/m3=6.97kg/m3
求通過(guò)噴油器的質(zhì)量流量:
qm=ρa(bǔ)*qa=(1.185*500*10-3/60)kg/s=0.009875kg/s
求截面積1和截面積2處的平均流速:
u1=qm(ρ1A1)=[0.009875/(6.97*0.785*0.0082)]m/s=28.2m/s
u2=qm(ρ2A2)=[0.009875/(6.97*0.785*0.00742)]m/s=33m/s
由伯努利方程課的:
p1-p2=0.5*ρ1(u22-u12)=0.5*6.97(332-28.22)pa=1014pa
吸油管內(nèi)為靜止油液,若能吸入喉部,必須滿足:
p1-p2≥ρgh
h≤(p1-p2)/ρg=1014/(800*9.8)m=0.129m
故
說(shuō)明油杯內(nèi)油面比喉部低129mm以上便不能?chē)娪汀?
